The Air Film of an Antibubble
Jessica Chang
Introduction
What is an Antibubble?
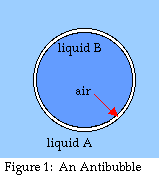
 An antibubble is the exact inverse of a
normal soap bubble (see fig. 1). Whereas a regular bubble is a pocket
of air or gas within a film or layer of liquid, the whole thing
surrounded by gas, an antibubble is a pocket of
liquid enclosed within a layer of gas, the whole thing surrounded by
liquid (Connett 1974, Nadovich 1999, Beaty 1999). Antibubble
formation is an intriguing natural phenomenon, the physics of which are
complex and not yet fully known (Connett 1974, Nadovich 1999). Somehow
a thin layer of air becomes trapped around a drop of liquid when it
falls on the surface of another liquid. Often a “boule”, or a floating drop, forms on the
surface. An antibubble forms when the drop becomes totally submerged
(see fig. 2). If the drop contains a denser solution, the antibubble
formed will actually sink to the bottom of the vessel.
An antibubble is the exact inverse of a
normal soap bubble (see fig. 1). Whereas a regular bubble is a pocket
of air or gas within a film or layer of liquid, the whole thing
surrounded by gas, an antibubble is a pocket of
liquid enclosed within a layer of gas, the whole thing surrounded by
liquid (Connett 1974, Nadovich 1999, Beaty 1999). Antibubble
formation is an intriguing natural phenomenon, the physics of which are
complex and not yet fully known (Connett 1974, Nadovich 1999). Somehow
a thin layer of air becomes trapped around a drop of liquid when it
falls on the surface of another liquid. Often a “boule”, or a floating drop, forms on the
surface. An antibubble forms when the drop becomes totally submerged
(see fig. 2). If the drop contains a denser solution, the antibubble
formed will actually sink to the bottom of the vessel.
Purpose:
According to Connett (1974) and Wismer (1999), the air volume fraction
of an antibubble is not a constant. Connett hypothesized that this was
because the air layer absorbed dissolved gases from the surrounding
solutions over time. However, these report s did not actually measure
the air volume fractions. The purpose of this
experiment is to test the hypothesis that the air volume fraction of an
antibubble is a constant. A new method to calculate the volume
proportion of th e air layer to the whole antibubble will be used to
test this hypothesis.
Theory:
Based on theoretical calculations and several key assumptions, the
volume fraction of air in an antibubble can be found using the following
formula:
density of interior liquid - density of bath liquid
--------------------------------------------------- = volume fraction of air
density of interior liquid
This formula is an extrapolation of the idea that the density of an object is a combination, by volume proportions, of the densities of its components. The mathematical derivation goes as follows (next page):

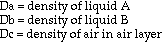
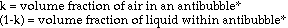
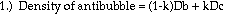
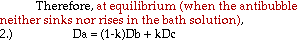

Approximations and assumptions made in deriving this formula:
1. The density of the entire antibubble is the simple relationship indicated in equation 1, with negligible interaction between air and liquid.
2. The density of the air is much smaller than those of the liquids, such that it is essentially zero for the derivation of the final two equations.
3. The pressure of the surrounding liquid acting on the volume of the antibubble is negligible near the surface of the bath liquid.
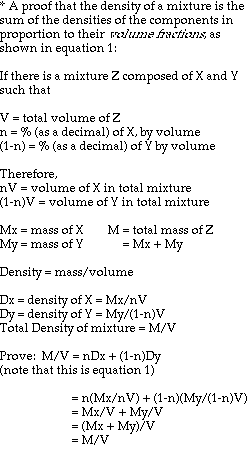
Procedure:
The surrounding (bath) solution was designated “Liquid A.”
Liquid A was composed of 0.25mL of Palmolive dishwashing detergent per
liter of distilled water. The liquid inside the antibubble was
designated “Liquid B.” This liquid was composed of liquid A
plus varying amounts of salt to change the density. An antibubble was
formed by dropping 0.02-0.03 mL drops of liquid B from a height of 3 cm
from a 1 mL graduated pipette into a test tube with 20 mL of liquid A.
The test tubes used were 17.5 cm tall with an inside diameter of 2.0 cm.
The 20 mL of liquid A in the test tubes formed a column of liquid about
7 cm high. The densities of liquids A and B were determined by massing
(to 0.001g) 10.00 mL (by volumetric pipette) of each solution.
In theory, equilibrium would be considered achieved when the
antibubble neither rose or sank. However, in practice,
antibubbles rarely stay stationary in the bath. For every antibubble
that formed, it was recorded on which drop it was formed and whether it
rose, sank, or sank and then rose. Most of the time, antibubbles did
not form on the first drop. Additional drops were added to each test
tube until an antibubble formed. This was repeated f or each solution
of liquid B. Concentrations of salt in liquid B ranged from 0.15M to
0.50M NaCl, by 0.05M increments.
The highest and the lowest B densities
that would form an antibubble that sank and/or rose were used to
calculate the range of plausib le volume fractions of air in the
antibubble using Equation 3.
The results of this procedure were
tested against those from an alternate method, proposed by Connett
(1974). This method required the formation of an antibubble (by
dropping liquid A into liquid A) in an overflowing flat-bottomed
container. Once the an tibubble formed, the container would be capped
without trapping any other air and inverted so that the antibubble rises
to the flat surface so that the diameter could be measured. This proved
very difficult. Thus, instead of capping and inverting, the vessel
remained upright and the diameters of both the antibubble and the
resulting regular air bubbles (when the antibubble popped) were measured
simply and roughly by holding a ruler over the open surface. The volume
fraction of air in the antibubble wa s then found by dividing the volume
of the air bubble by that of the entire antibubble.
Results:
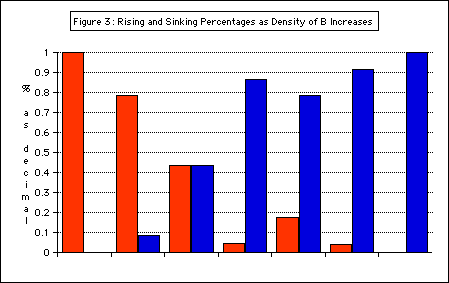
Figure 3: Rising and Sinking Percentages as the density of B increases
 indicates % of antibubbles that rose
indicates % of antibubbles that rose
 indicates % of antibubbles that sank
indicates % of antibubbles that sank
This graph shows the dual behavior of antibubbles made from the same solutions — evidence for a range of volume fractions, shown in purple.
The range of plausible volume fractions of air was determined using this data (Figure 4).
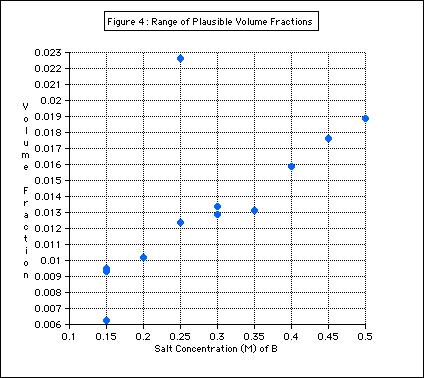
Figure 4: The purple bar in this graph shows the range of volume
fractions of air. This was made by including the B solutions in the
purple zone of the graph above.
Connett’s method was then tested to see if these results could be
replicated. Connett’s method proved very difficult, however, and
the results were very inaccurate. The diameter of the antibubble could
only be determined to be about 4mm, and t he resulting air bubble was
less than 1mm, greater than .7cm. Despite these imprecisions, the
results generated by further calculations fall mostly within the
predicted range. Generally, the antibubbles formed were brief and they
all hung at the top. F or this reason, only the minimum side of the
spectrum can be shown with these results.
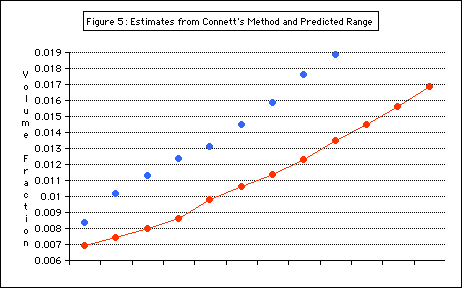 Results from
Connett’s method, though imprecise, fall mostly into the r
ange predicted (Figure 5).
Results from
Connett’s method, though imprecise, fall mostly into the r
ange predicted (Figure 5).
Figure 5 shows the air volume fraction results from the first method as blue dots and from Connett’s method as the connected red dots. The results from Connett’s method mostly fall within the range predicted by the first method (sh
own with a purple bar)
The results of the experimental method agreed with those obtained from the alternate (Connett’s) method. The range of air volume fraction values for antibubbles containing a 0.02-0.03 mL drop was found to be from 0.009 to about 0.017, or 0.9 - 1.7%
of the entire antibubble volume.
Discussion:
Although the result of this preliminary study showed a very small range of values for the calculated air volume fraction, the maximum is almost double the minimum. This variation could be due to several factors as discussed below:
1. During this study, it was observed that some antibubbles first sank, then rose: their densities must have been changing. Since the liquid inside the antibubble cannot change volume or escape, then the air volume must be
changing to affect the total density of the antibubble. To explain this observation, Connett proposed that the antibubbles absorb dissolved air molecules from the bath liquid and thus become less dense as they sit in the bath. This phenomenon cou
ld account for some of the variations in this study.
2. The distance that liquid B was dropped from was only approximate, and may not have remained constant throughout experimentation. The amount of air trapped initially may depend on this height.
3. In this preliminary study, only one solution A was tested. The small range of calculated results may simply be due to measuring errors. Whether the range obtained in this study is constant requires further experimentatio
n using different A solutions. At least two more A solutions of different densities must be tested to see whether the range of this experiment can be duplicated, whether it is a constant (see Figure 6).
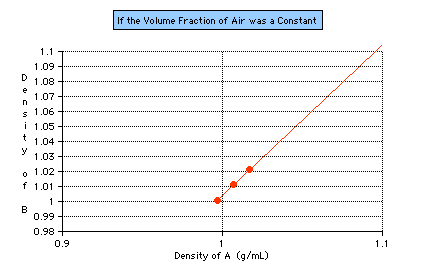
Figure 6: A hypothetical graph of what one would expect if the volume fraction of air in an antibubble were really a constant range. The first point plotted indicates the range obtained from this study. The second point (using the same procedure with a
different A solution), is currently being investigated.
Conclusions:
1. The volume fraction of air film in the antibubble can be calculated from the densities of the solutions that are used to form the antibubbles at equilibrium.
2. The volume fraction of air film in antibubbles ranges from 0.9 to 1.7% of the entire antibubble volume.
References:
Beaty, Bill. “Making Antibubbles.” n.d.; n.pag.
Online. Internet. 12 Sept. 1999. Available:
http://www.eskimo.com/~billb/amateur/antibub/antibub1.html
Boys, C. V. Soap Bubbles and the Forces Which Mould Them. New York: Doubleday & Company, Inc. 1959.
(This does not discuss antibubbles, but is a very good book on regular bubbles and many of their scientific properties.)
Nadovich, Chris. “Antibubbles.” n.d.; n.pag. Online. Internet. 12 Sept. 1999. Available:
http://www.jtan.com/antibubble
(This source includes a
link to project notes from Timothy Wismer, who did a school science project on antibubbles in 1999.)
Strong, C. L., Connett, J. E. “The Amateur Scientist: Curious Bubbles in which a Gas Encloses a Liquid Instead of the Other Way Around.” Scientific American Aug. 1974: 117-121.
Acknowledgements:
First, I would like to thank my father for his incredible moral support. I would also like to acknowledge Chris Nadovich, the creator of the Antibubble website which inspired this project.


|
B solution
|
test tube #
|
Description
|
|
O.15
|
8
|
hung at top, long-lasting
|
|
|
20
|
hung at top, brief
|
|
|
21
|
hung at top, brief
|
|
0.2O
|
9
|
hung 1cm from top, brief
|
|
|
17
|
slowly up to hang on top, long-lasting
|
|
O.25
|
9
|
hung on top, brief
|
|
|
15
|
too brief to tell
|
|
0.3O
|
5
|
sank, popped on touching bottom
|
|
O.35
|
5
|
too brief to tell
|
|
|
19
|
slowly sank 1.5cm
|
|
|
21
|
very slowly sank 2.5cm, pause, rose 1.3cm
|
|
0.4O
|
1
|
too brief to tell
|
|
|
8
|
sank, very brief
|
|
|
12
|
hung at top, brief
|
|
O.45
|
17
|
settled on bottom briefly
|
|
O.5O
|
0
|
none
|
|
B solution
|
B density
|
Volume Fraction
|
|
.15B
|
0.9979
|
0.00932
|
|
.15B
|
0.9913
|
0.009482
|
|
.15B
|
1.0033
|
0.00627
|
|
.20B
|
0.9988
|
0.01021
|
|
.25B
|
1.0035
|
0.02262
|
|
.25B
|
1.001
|
0.01239
|
|
.30B
|
0.9952
|
0.01336
|
|
.30B
|
1.0111
|
0.01286
|
|
.35B
|
1.0114
|
0.01315
|
|
.40B
|
1.0142
|
0.01587
|
|
.45B
|
1.0149
|
0.01764
|
|
.50B
|
1.0173
|
0.01887
|
|
Results (Estimates) from Connett's Method
|
|
|
|
|
|
|
Antibubble
|
bubble
|
volume fraction of air
|
|
|
|
|
3.9
|
1
|
0.01685
|
0.00691
|
0.008357
|
|
|
3.9
|
0.9
|
0.01229
|
0.00743
|
0.01021
|
0.00691
|
|
3.9
|
0.8
|
0.00863
|
0.008
|
0.0113
|
0.00984
|
|
4
|
1
|
0.0156
|
0.00863
|
0.01239
|
0.0135
|
|
4
|
0.9
|
0.0114
|
0.00984
|
0.01311
|
0.00743
|
|
4
|
0.8
|
0.008
|
0.0106
|
0.01449
|
0.0106
|
|
4.1
|
1
|
0.0145
|
0.0114
|
0.01587
|
0.0145
|
|
4.1
|
0.9
|
0.0106
|
0.01229
|
0.01764
|
0.008
|
|
4.1
|
0.8
|
0.00743
|
0.0135
|
0.01887
|
0.0114
|
|
4.2
|
1
|
0.0135
|
0.0145
|
|
0.0156
|
|
4.2
|
0.9
|
0.00984
|
0.0156
|
|
0.00863
|
|
4.2
|
0.8
|
0.00691
|
0.01685
|
|
0.01229
|
|
|
|
|
|
|
0.01685
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
page #

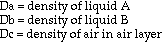
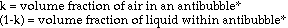
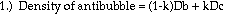
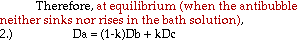

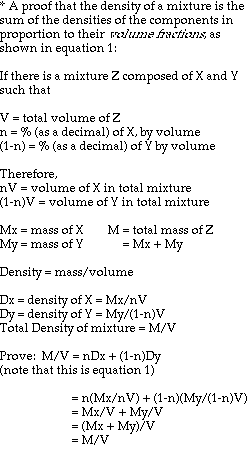

 An antibubble is the exact inverse of a
normal soap bubble (see fig. 1). Whereas a regular bubble is a pocket
of air or gas within a film or layer of liquid, the whole thing
surrounded by gas, an antibubble is a pocket of
liquid enclosed within a layer of gas, the whole thing surrounded by
liquid (Connett 1974, Nadovich 1999, Beaty 1999). Antibubble
formation is an intriguing natural phenomenon, the physics of which are
complex and not yet fully known (Connett 1974, Nadovich 1999). Somehow
a thin layer of air becomes trapped around a drop of liquid when it
falls on the surface of another liquid. Often a “boule”, or a floating drop, forms on the
surface. An antibubble forms when the drop becomes totally submerged
(see fig. 2). If the drop contains a denser solution, the antibubble
formed will actually sink to the bottom of the vessel.
An antibubble is the exact inverse of a
normal soap bubble (see fig. 1). Whereas a regular bubble is a pocket
of air or gas within a film or layer of liquid, the whole thing
surrounded by gas, an antibubble is a pocket of
liquid enclosed within a layer of gas, the whole thing surrounded by
liquid (Connett 1974, Nadovich 1999, Beaty 1999). Antibubble
formation is an intriguing natural phenomenon, the physics of which are
complex and not yet fully known (Connett 1974, Nadovich 1999). Somehow
a thin layer of air becomes trapped around a drop of liquid when it
falls on the surface of another liquid. Often a “boule”, or a floating drop, forms on the
surface. An antibubble forms when the drop becomes totally submerged
(see fig. 2). If the drop contains a denser solution, the antibubble
formed will actually sink to the bottom of the vessel.

 indicates % of antibubbles that rose
indicates % of antibubbles that rose  indicates % of antibubbles that sank
indicates % of antibubbles that sank
 Results from
Connett’s method, though imprecise, fall mostly into the r
ange predicted (Figure 5).
Results from
Connett’s method, though imprecise, fall mostly into the r
ange predicted (Figure 5).

